二項定理 係数 問題 250280-二項定理 係数 問題

 · 今回は東大がよく出題する二項係数に関する整数問題をイメージして作問しました。 問題はこちら（画像をクリックするとPDFファイルで開きます。 ） 仮想難関大シリーズということで、東大、京大をはじめとする旧帝大、東工大、国公立大学医学部医学科などの難関国公立大を想定した · 二項定理 (xy) 3 を展開した時の「x 2 y」の係数はいくつかというと、公式「(xy) 3 ＝x 3 3x 2 y3xy 2 y 3 」を思い出せば「3」と分かります。 しかし (xy) 10 を展開した時の「x 2 y 8 」の係数はいくつになるかは公式を覚えていないし実際に展開するのは面倒くさいですね。 。これを簡単な計算で · 二項定理の問題でよく出てくるのが、係数を求める問題。 ですが、上で説明した二項定理の意味がわかっていれば、すぐに答えが出せるはずです。 問題1(xy)⁵の展開式における、次の項の係数を求めよ。

二項定理 多項定理 ２０１７年前期日程の新潟大学理学部 工学部入試問題 身勝手な主張

二項定理 係数 問題

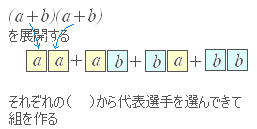
二項定理 係数 問題-二項係数 (n k) の場合、とりあえずn は固定して、数列 (n 0);なぜ a r b n−r にしないのか？ n C r = n C n−r が成り立つので，どちらで考えてもよい．ただし，多くの教科書や参考書では，上に書いた形（ b の係数が増える順）に書いてある． （二項定理の解説） 通常，式の展開は次のような順序で，「総当たりで」掛けると考えることが多いが，二項定理，多項定理の解説はこの方法では分かりにくいので，「代表選手の選び方

二項定理 公式の証明や係数の求め方を解説 基礎から大学受験まで Studyplus スタディプラス

(n n) の母関数、つまり次の多項式を考えます。 ∑n k=0 (n k) xk= (n 0) (n 1) x (n 2) x2 (n n) xn (n k) の母関数は次のような性質を満たします。 定理14 (二項定理) 任意の非負整数n と文字x に対して ∑n k=0 (n k) xk = (1 x)n 練Appendix 二項定理 二項定理とは、(a b)n の展開式を求める公式である。n は任意の自然数だが、a;b は任意の複 素数でよい。 POINT (二項定理) (a b)n を展開したときの、akbn k の展開係数はnCk で与えられる。 したがって、 (a b)n = nC0 an nC1an 1b1 ・・・・・nCn 1a1bn 1 nCn bn =∑n k=0 nCka kbn k 二項定理の数学における二項係数（にこうけいすう、英 binomial coefficients ）は二項展開において係数として現れる正の整数の族である。 二項係数は二つの非負整数で添字付けられ、添字 n, k を持つ二項係数はふつう () と書かれる（これは二項 冪 (1 x) n の展開における x k の項の係数である。

 · 二項定理の公式にC (コンビネーション)が出てくる理由 #1の右辺の各項の係数を見ると、 (1、3、3、1) となっています。 これはaの三乗を作るためには (ab) (ab) (ab)の中からa掛けるa掛けるaを 選び出す しか無く、その 場合の数を求める為にCを使っている のです。 この場合では1通りなので (1)・ (a^3)となっています。 同様に、 a 2 bの係数を考えると、（ab) (ab) (ab二項定理 (binomial theorem) と聞けば，数学者なら，Newton の一般二項定理 (01) $(1t)^{x}= \sum_{n=0}^{\infty}Matrix t^{n}$ をまず思うだろう．但し，二項係数は $Matrix= \frac{x(x1)\cdots(xn1)}{n!}$ と定義される．この有用な公式自体はもちろん，今回も後に活躍する．しかし，タイトルに 関わる二項定理，三項定理は，むしろ高校生の思い浮かべるものと言ってよい二項定理 を用いて" (x＋y)⁴"を展開していきます。 (x＋y)⁴=x⁴4x³y6x²y²4xy³y⁴ 以上から、 {xy³}の係数は4とわかります。 この問題のように指数が小さいときは、 二項定理 を用いて式を展開しさえすれば簡単に係数を求めることができます。 しかし、" (x＋y)⁹"のように展開するのが面倒くさい場合はどうでしょう。 すべて展開するにはちょっと時間がかかり

 · 二項定理の式の意味 では例として\((ab)^4\)について考えてみましょう。 $$(ab)^4=(ab)(ab)(ab)(ab)$$ ですね。この式を展開しなさいと言われるとちょっとめんどくさいですよね。そんな時に使えるのがこの二項定理になります。 · 二項定理の係数問題は、求める係数の次数と二項定理の一般項を比較して、 \({}_n\mathrm{C}_r\) の \(r\) が求まれば一発です。 (3) \((a2b3c)^5\) における \(a^2b^3\) の係数を二項定理－係数から指数を求める－ ALL モード n を2以上の自然数とする。 ( 1 2 x) n の展開式における x 2 の係数が60となるとき， n の値を求めよ。 3 4 6

二 項 定理

二項級数 Binomial Series Japaneseclass Jp

About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators(n − r − 1)!r!二項定理の応用(2) 割った余りを求める問題 19年12月25日 二項定理を利用すればとても大きな数(累乗数)について調べることも容易になります。

12 二項定理 多項定理 京極一樹の数学塾

二項定理ってなんだよ 多項定理ってなんだよ ってなっている君へ

 · k k まで正しいと仮定すると，二項定理より， ( x 1 ⋯ x k x k 1) n = { ( x 1 ⋯ x k) x k 1 } n = ∑ t = 0 n n C t ( x 1 ⋯ x k) t x k 1 n − t (x_1\cdots x_kx_ {k1})^n\\ =\ { (x_1\cdots x_ {k})x_ {k1}\}^n\\ =\displaystyle\sum_ {t=0}^n {}_n\mathrm {C}_t (x_1\cdots x_ {k})^tx_ {k1}^ {nt} (x1 ⋯ xk(1) 二項係数の定義により, \\begin{aligned} k\,{}_p\mathrm C_k &= k\cdot\frac{p!}{k!(pk)!} \\ &= k\cdot\frac{p}{k}\cdot\frac{(p1)!}{(k1)!\{ (p1)(k1= (n − 1)!(n − r) (n − r)!r!

この展開式の定数項の求め方を教えてくださいm M 二項定理を使うん Yahoo 知恵袋

二項定理 多項定理 ２０１７年前期日程の新潟大学理学部 工学部入試問題 身勝手な主張

Try IT（トライイット）のnCr と2項定理の映像授業ページです。Try IT（トライイット）は、実力派講師陣による永久0円の映像授業サービスです。更に、スマホを振る（トライイットする）ことにより「わからない」をなくすことが出来ます。全く新しい形の映像授業で日々の勉強の「わからない重要 二項定理の公式： n C r a n−r b r において， a n−r, b r については 「係数も何乗かする」ことが重要 係数 何乗 × n C r が係数になる 負の数を奇数乗すると負の数になる． · 二項定理について 二項定理と聞いてなんだっけと思う人は多いと思いますし、この記事を見てくださっている人はその 1 人なのではないでしょうか。 そもそも二項定理とはなんなのかを知り、さらに二項定理の導出を踏まえて使い方を学んでいきましょう。

1

二項定理 多項定理 Youtube

 · 二項係数の有名公式一覧と2つの証明方針 レベル ★ 最難関大受験対策 場合の数 二項定理 更新日時 二項係数の有名公式を紹介していきます。 二項係数の関係式を証明するための2通りのアプローチを紹介します。 · 二項定理は意味よりも公式化されたものを暗記しているのではないでしょうか。 しかし、公式の形がシグマで表されているので覚えにくく使えない状態の人が多くいます。 一般項の見方と2項展開したときの係数の求め方を具体的な問題を使二項定理とは パスカルの三角形を利用して、次の定理を導くことができます。 (ab)ⁿ=nC₀aⁿnC₁aⁿ⁻¹bnC₂aⁿ⁻²b²nCraⁿ⁻ʳbʳnCn₋₁abⁿ⁻¹nCnbⁿ ※nCrのnとrは下付き文字 この定理を 二項定理 といいます。 指数の数が大きいときに、この定理は力を貸してくれます。 では早速、二項定理を用いて次の問題を解いてみましょう。

はさみうちの原理を使う問題で二項定理を使うコツを限定公開

二項定理 公式の証明や係数の求め方を解説 基礎から大学受験まで Studyplus スタディプラス

問題 (2x 23) 7 を展開して整理したとき、x 10 の係数を求めよ。 解答 (2x 23) 7 = 7 C r (2x 2) 7r ・(3) r x 10 の項は 2(7r)＝10 つまり、r＝2 のとき得られる。 7 C 2 (2x 2) 5 ・(3) 2 ＝6048x 10 よって、求める係数は 6048 また、合わせて多項定理もおさえておきましょう。二項定理の応用 二項定理は非常に汎用性が高く実に様々な分野で応用されます．数学の別の定理を証明するために使われたり，数学の問題を解くために利用することもできます． 剰余 累乗数のあまりを求める問題に応用できる場合があります．数え上げの基礎：二項係数と二項定理 岡本吉央 okamotoy@uecacjp 電気通信大学 15年10月6日 最終更新：15年10月21日0852 岡本吉央(電通大) 離散数理工学(1) 15 年10 月6 日 1 / 64 概要 概要 主題 次の3つを道具として

2講 二項定理 1節 式と計算 問題集 1章 式と証明

12 二項定理 多項定理 京極一樹の数学塾

2 二項係数の関係式（1） 問題1 n を正の整数とするとき，次の等式を証明せよ． (1) nCr = n−1Cr n−1Cr−1 (1 5 r 5 n − 1) (2) (a b)n = ∑n r=0 nCra n−rbr （解答）(1) n−1Cr n−1Cr−1 = (n − 1)!2 二項係数\({}_n\mathrm{C}_r\)の重要公式3つ 21 残りを考える式;(n − r)!(r − 1)!

二項定理 多項定理 ２０１７年前期日程の新潟大学理学部 工学部入試問題 身勝手な主張

今日の問題 3 二項定理や二項係数を利用し フェルマーの小定理 を証明する 高校2年生以上推奨 Aggressive Style

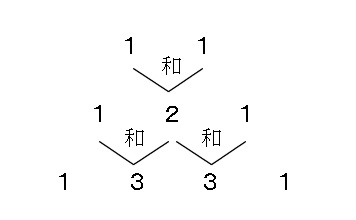
 · 多項定理と二項定理を展開したときの各項の係数を決める方法です。 多項定理の一般項は公式としては覚えにくいです。 定理なので覚えている場合はそのまま使って構いませんが、覚えていない場合あきらめるにはもったいないので二項定理 · つまり、 累乗の数はあまり大きくないときは、このパスカルの三角形を書いて二項係数を求めたほうが早く求められます！ ですので、パスカルの三角形は便利なので、場合によっては利用するのも手です。 4 二項定理を利用する問題（係数を求める問題） · 二項係数の和について説明します。 結局は「係数の和」ですから，何らかの多項式を考えることになります。 大学入試で出題される数学の問題を解くときの着眼点・考え方・解法の糸口の掴み方を伝えます。

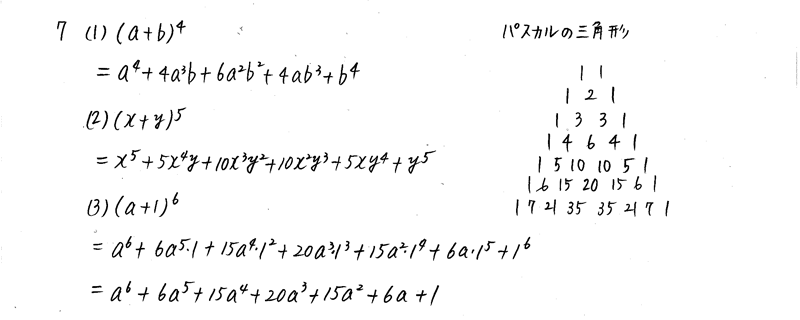
新課程 3trial数学 P7 ２ 二項定理

二項定理の公式と証明をわかりやすく解説 公式 証明 係数 問題

0215 · こちらを二項定理を使って展開をしていくと、 一般項は次のような形になり、 になるための の値を見つけることができます。 になることが分かれば、一般項にあてはめて計算をしていきましょう。 よって、 の係数は であることが求まりました。 答え （2）の解説、約分ができるので注意！ 定数項は？ 問題 （2） 定数項1029 · 目次 1 二項係数\({}_n\mathrm{C}_r\)の基本を確認 11 組合せとは;一二項宗理の理解を深めるために一 数学科川谷内哲二 二項係数に関する等式は，主に二項定理を利用して取り扱うが，生徒の理解が十分でない。そこで， パスカルの三角形を考察することによって，二項定理の理解を深めることをねらいとした。本稿は，パ

二項係数 Wikipedia

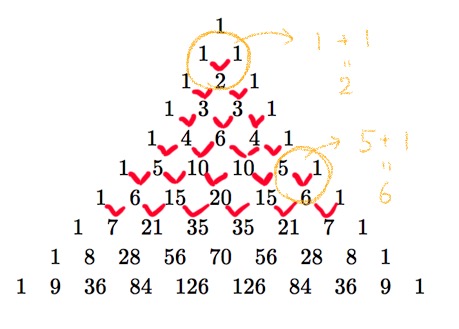
差がつくポイント 二項定理はイメージで覚えろ 重要なポイントと活用場面を総まとめ 青春マスマティック

1129 · 二項定理を使いたい不等式 二項定理は、基本的に「ナントカのn乗」を展開する際に利用できる定理です。これを踏まえれば、 二項定理を利用したくなる場面は、不等式に「ナントカのn乗」が含まれる時 です。 しかし、いつでもこれを使えばよいかというと、そうではありません。二項定理 *(二項展開 *(' 二項定理の応用 ** 多項係数と多項展開 * 一般化二項係数（組合せの個数の一般化） * 多項式を用いた組合せの個数の計算 *) 乱列と全射関数の個数 問題 分割：集合と整数の分割 本章の目標 ウォーミングアップ問題 ' ウォーミング二項定理による係数・定数項の求め方 例題①「係数を求める」 例題②「定数項を求める（分数を含む式）」 例題③「定数項を求める（分数を含む式）」 参考パスカルの三角形;

二項定理のしくみと意味 A B のn乗 高校数学なんちな

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

(a b) n の係数は，上述した具体的な計算事例と k C r k C r − 1 = k 1 C r の関係から，パスカルの三角形が得られる． パスカルの三角形を下に示す． ホーム>>カテゴリー分類>>数列>>数列：二項定理 初版：04年7月6日，最終更新日： 13年10月24日

二項定理の基本 Youtube

高校数学無料問題集 数 第１章 式と証明 二項定理 多項定理 桝 ます Note

数学 B 二項定理に関する入試問題 昭和薬科大 愛知大 成蹊大 近畿大 大学入試数学の考え方と解法

高校数学無料問題集 数 第１章 式と証明 二項定理 多項定理 桝 ます Note

パスカルの三角形と二項定理による展開との関係とは 二項係数の性質を証明 遊ぶ数学

パスカルの三角形と最短経路 思考力を鍛える数学

二項係数とその和 難関大学への数学

志錐館ブログ 大阪の予備校 塾

２項係数の性質

二項定理 二項係数の性質を研究する 余りを求める 大人が学び直す数学

式と証明 二項定理について 日々是鍛錬 ひびこれたんれん

二項定理 の係数を求める問題を中心に 数学の偏差値を上げて合格を目指す

二項係数 難関大学への数学

二項定理の問題です 添付画像の 内の項の係数を求めろという問題なので Okwave

二項定理 公式の証明や係数の求め方を解説 基礎から大学受験まで Studyplus スタディプラス

二項係数とその和 難関大学への数学

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

二項定理とは 東大生が公式や証明問題をイチから解説 高校生向け受験応援メディア 受験のミカタ

二項定理を簡単に覚える 定数項 係数の求め方 高校数学の知識庫

二項定理 おいしい数学

式と証明 二項定理について 日々是鍛錬 ひびこれたんれん

多項定理の一般項と二項定理を利用した係数の求め方

12 二項定理 多項定理 京極一樹の数学塾

二項定理 7 問題 齊藤数学教室 算数オリンピックから大学数学入門

二項定理の係数を求める問題の解説 Youtube

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

二項定理と二項係数について 応用例題

数学a 二項 多項定理 係数を求める問題 チャート 実践例題集 自宅でできる受験対策ショップ ワカルー Wakaru

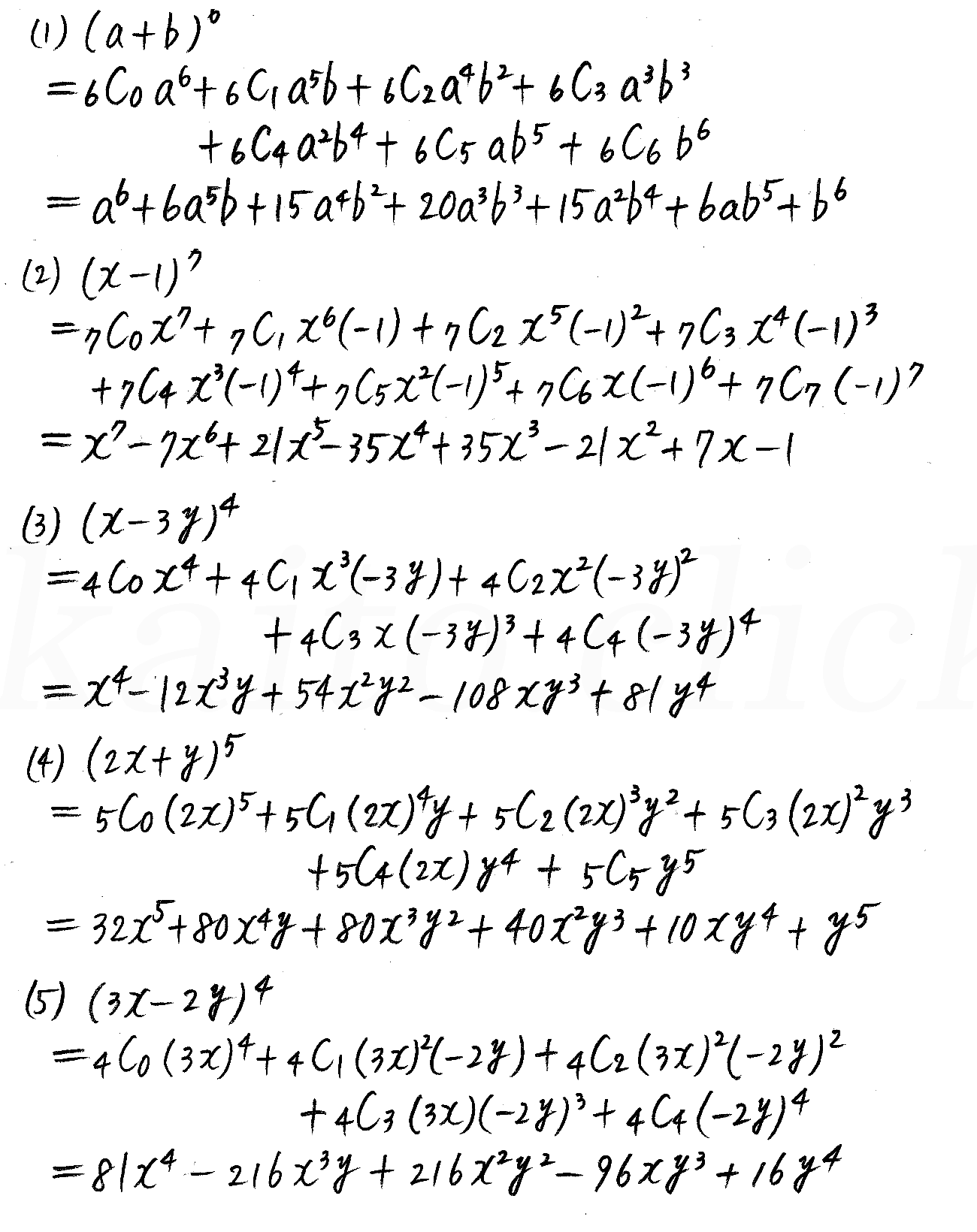
改訂版 クリアー数学 P7 ２ 二項定理

14の 2 の問題で展開式の一般項の右辺がなぜこうなるの分からないです はっきりとし Clear

高校数学 二項定理の応用 累乗数の余りと下位桁 受験の月

二項展開式の係数 大学受験の王道

二項定理の公式を超わかりやすく証明 係数を求める問題に挑戦だ 応用問題も解説 遊ぶ数学

12 二項定理 多項定理 京極一樹の数学塾

二項定理 は超重要な展開公式 場合の数から理解しよう

二項定理 近似計算

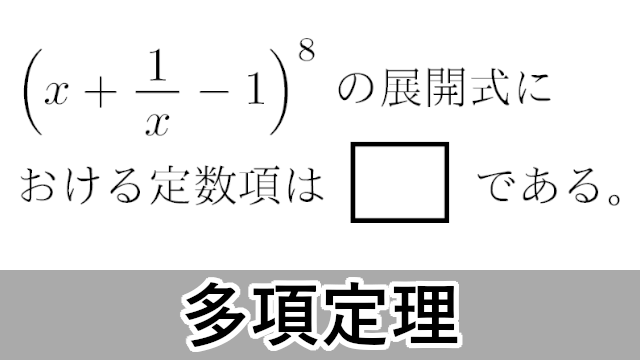
数学 B 多項定理 展開式の係数と定数項 北里大 愛知医科大 福岡大 大学入試数学の考え方と解法

二項定理を超わかりやすく解説 公式 証明 係数 問題 理系ラボ

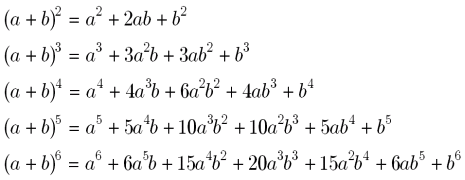
二項定理 二項定理とはなにか 大人が学び直す数学

数ii 二項定理 定数項の係数 Youtube

数学ii Bチェック リピート 第1章 1式と証明 5 二項定理の応用 Pukiwiki

Q二項定理 Wikipedia

二項定理を利用してsを使わない形にする例題 ばたぱら

12 二項定理 多項定理 京極一樹の数学塾

二項定理の問題なのですが 定数項の時は係数 1 となるのは何 Yahoo 知恵袋

二項係数

二項定理とは 証明や応用問題の解き方をわかりやすく解説 受験辞典

高校数学 数 勉強動画 二項定理 の問題 19ch

3

二項定理の定数項の求め方についてです Clear

多項定理 一枚目が問題で二枚目が解答です Clear

2

二項定理 公式 の一般項や２項展開係数の求め方

二項係数とその和 難関大学への数学

二項定理 多項定理

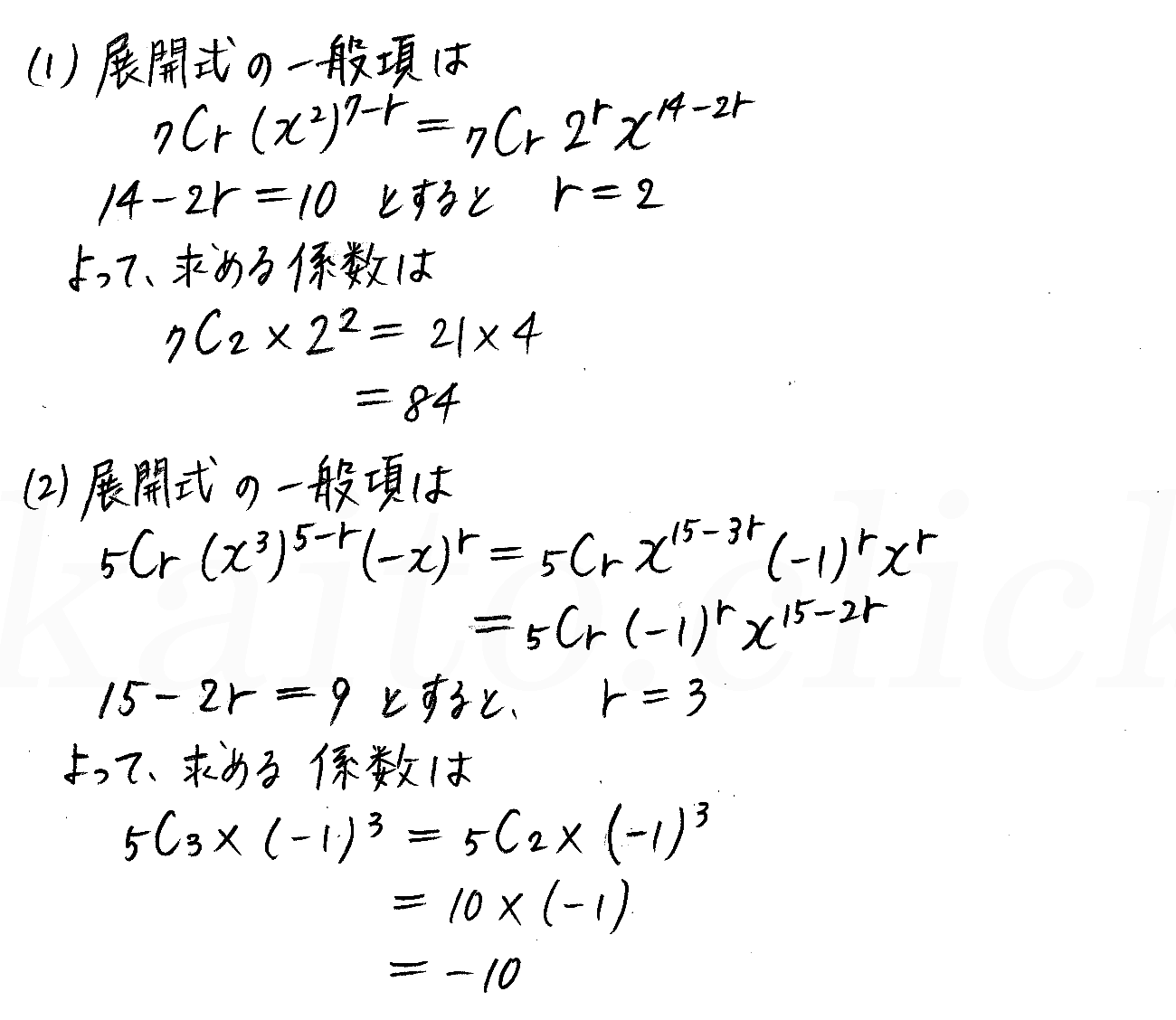
改訂版 クリアー数学 P8 ２ 二項定理

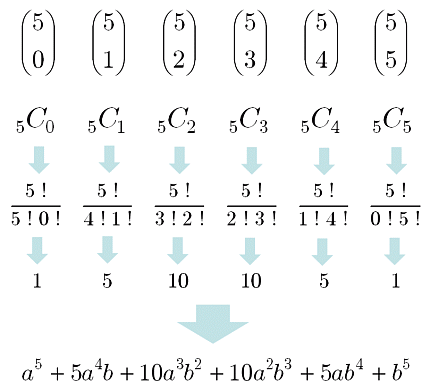
二項定理 二項係数 を計算する 大人が学び直す数学

先生 二項定理がよくわかりません 怜悧玲瓏 高校数学を天空から俯瞰する

鉄緑会数学講師のひとりごと 二項係数

２ 二項定理とその応用 Imujii S Page

高校数学 多項定理 A B C Nの展開式の係数 受験の月

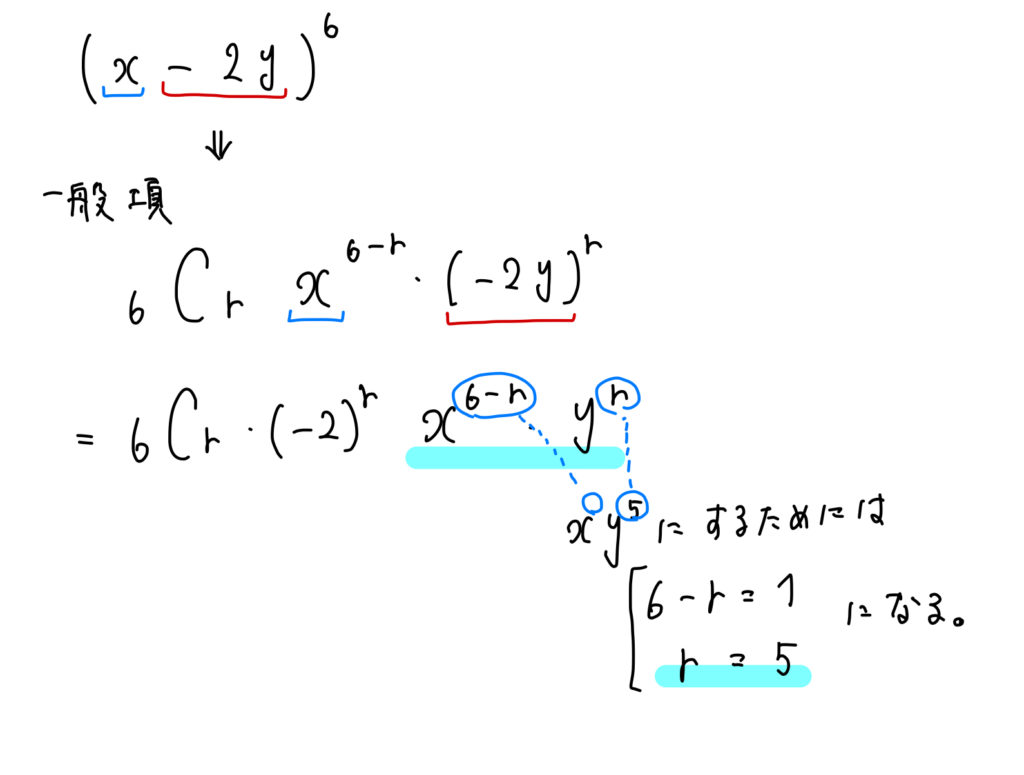
展開式の係数の求め方 二項定理を使ったやり方をイチからやってみよう 数スタ

3 と 4 教えてください 二項定理の問題です Clear

シグマ計算基本方針 第６講 二項係数の交代和 05年度 山形大学

多項係数 Japaneseclass Jp

二項定理 Cの係数を求めるところで なぜこのような数字になるのかわかりません Clear

組み合わせの公式２ 高校数学 二項定理周辺の公式 身勝手な主張

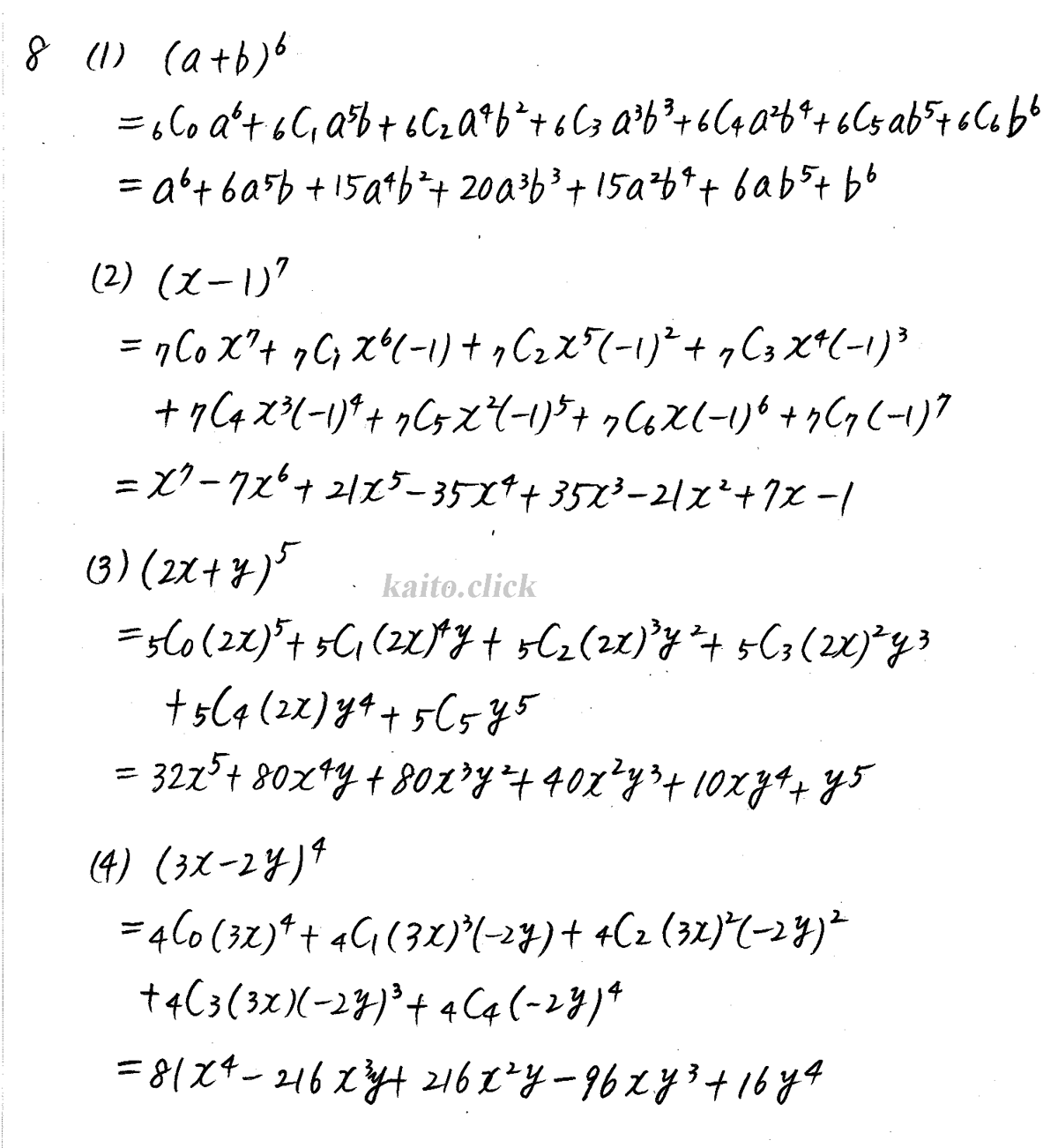
クリアー数学 数2 P7 ２ 二項定理

1

多項定理 はどんな定理 実は 二項定理 とほぼ同じ

二項定理とは 公式と係数の求め方 応用までをわかりやすく解説

1

東大数学ー二項係数の難問 1999年ー 虚空が数学をやるブログ

二項定理 Twitter Search

高校数学 二項係数ncrの和の等式 二項定理の利用 受験の月

大学入試数学の問題

二項定理の使い方３タイプ 怜悧玲瓏 高校数学を天空から俯瞰する

数 二項定理 Nck の和 オンライン無料塾 ターンナップ Youtube

数学用語解説 数a補足 二項定理 にこうていり

数学日誌 Math Diary 第8日目 二項定理の最大係数 Natural Style

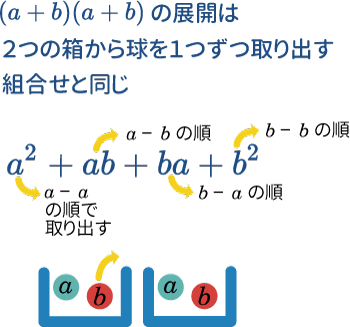
数 式と証明 二項定理は 箱からボールを選ぶ問題 として考える Mm参考書

二項定理の係数を求める問題です この先がわかりませんわかる Yahoo 知恵袋

高校数学 Ncr と２項定理 映像授業のtry It トライイット

二項定理の例題 5 齊藤数学教室 算数オリンピックから大学数学入門

Incoming Term: 二項定理 係数 問題,